こんにちは。
今回は、ディープラーニング(深層学習 Deep Learning)について、少しお話をしたいと思います。テレビなどでも「人工知能」に関するニュースが多くなってきましたが、いずれも、このディープラーニングという手法が背景にあるようです。
画像認識と強化学習(DQN)を中心とした、ディープラーニングの書籍「実装 ディープラーニング」をオーム社から出版しました。詳しくはこちらをご覧下さい。
まずは、簡単な一次関数の問題から始めます。
問題 1 2点P(1, 1)、Q(3, 4)を通る1次関数 \(y = ax + b\) について \(a\)、\(b\)の値をそれぞれ求めましょう。
これは、中学校で勉強する1次関数についての問題です。次のような連立方程式を解けばよいですね。
\[
\left\{
\begin{eqnarray}
a + b &=& 1 \\
3a + b &=& 4
\end{eqnarray}
\right.
\]
これを解いて、傾き \(a = 1.5\) 、切片 \(b = -\ 0.5\) となります。求める1次関数は、
\[
y = 1.5x\ -\ 0.5
\]
です。
この1次関数をグラフにかくと、次のようになります。2点をピッタリ通る直線を1本ひくことができます。
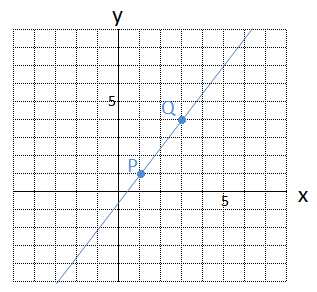
この求めた1次関数 \(y = 1.5x\ -\ 0.5\) は、入力層のユニット数が1、出力層のユニット数が1の、簡単なニューラルネットワークとも言えますね。
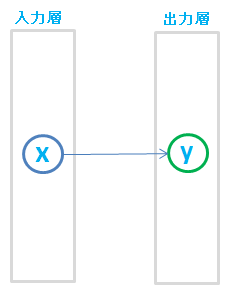
それではもう1問。通過すべき点を、さらに2個増やしてみます。
問題 2 4点P(1, 1)、Q(3, 4)、R(5, 4)、S(7, 8)を通る1次関数 \(y=ax+b\) について \(a\)、\(b\) の値をそれぞれ求めましょう。
この4点をグラフに表すと、次のようになります。
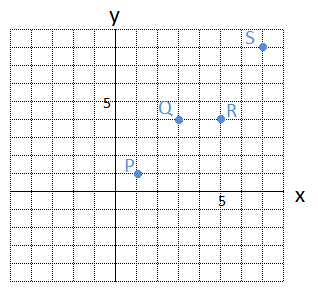
この4点をピッタリと通る1次関数、すなわち 直線 は、はたしてあるのでしょうか?
答は 「 NO 」 です。
残念ながら、この4点をピッタリ通る直線は、ひくことができません。ですので、このような不都合な問題は、中学校や高校の勉強にはでてこないことになります。
これを連立方程式としてみてみましょう。
\[
\left\{
\begin{eqnarray}
a + b &=& 1 \\
3a + b &=& 4 \\
5a + b &=& 4 \\
7a + b &=& 8
\end{eqnarray}
\right.
\]
この連立方程式は、未知数が2個( \(a\) と \(b\) )、方程式が4本なので、やはり解くことはできません。
中学校で勉強する連立方程式は、未知数(パラメータの数)が2個であれば、方程式の数も2本でなければなりません。問題2は、方程式の数が多すぎるということになります。
とは言え、実際の世の中の現象は、このようにデータがバラバラなケースのほうが多いですよね。
そこで、4点をピッタリ通る直線がひけないのならば、なるべく4点の近くを通る直線をひいてしまおう、という考え方がでてきます。
次のように、多少誤差があってもよいから、直線をひいてしまおうというものです。直線を引くことができれば、\(x\) が6の時は、\(y\) はおよそ6.2程度だろうと推測することができるようになり、とても便利です。
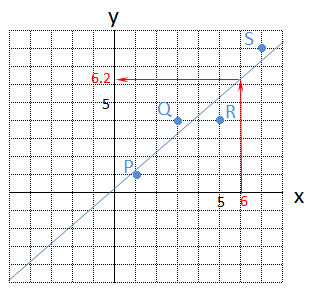
このような、(近似的な)直線のパラメータ \(a\)、\(b\) を計算する方法は、次のようにいくつかあります。
- ①単純に逆行列を利用して見つける方法
- ②推定値との差が最小になるようにパラメータを求める方法(最小二乗法)
(2)データを入手するたびに、パラメータを更新していく
- ③推定値との差が次第に小さくなるようにパラメータを求め、データを入手するたびにパラメータを逐次更新していく方法
データ量が膨大になると、上記の①や②の方法ではシステムの対応が難しくなるため、③の方法でパラメータを求める方法が便利です。③の方法は、データが毎日切れ目なく入ってくる場合でも、入ってくるデータのみを利用し、パラメータを順次更新することができるので、とても重宝されています。
ここでは、③の方法を紹介します。これは、(確率的)勾配降下法でという手法で、ディープラーニングでパラメータを計算するときも利用されています。
勾配降下法の概要
4点P(1, 1)、Q(3, 4)、R(5, 4)、S(7, 8)を(なるべく)通る1次関数 \(y=ax+b\) を求めるために、これを連立方程式の形で一旦表わしてみます。
\[
\left\{
\begin{eqnarray}
a + b &=& 1 \\
3a + b &=& 4 \\
5a + b &=& 4 \\
7a + b &=& 8
\end{eqnarray}
\right.
\]
この連立方程式を、行列で表現してみます。\(Xw\)(Xとwの内積)が推計値で、\(t\) が教師データ、すなわち、与えられた \(y\) の値です。
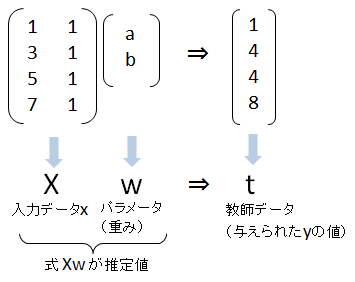
今の目標は、推計値と教師データの差がなるべく小さくなるように、\(w\) を求めることです。
このため、次のように \(E\) を定義し、\(E\) がなるべく小さくなるように、\(w\) を求めることにします。
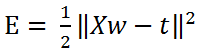
勾配降下法は、\(w\) に対する \(E\) の勾配 \(\Delta E\)(\(E\) を \(w\) で微分したもの)を求め、勾配が正であれば \(w\) を負の方向へと更新し、逆に勾配が負であれば \(w\) を正の方向に更新するという、とてもシンプルな考え方です。
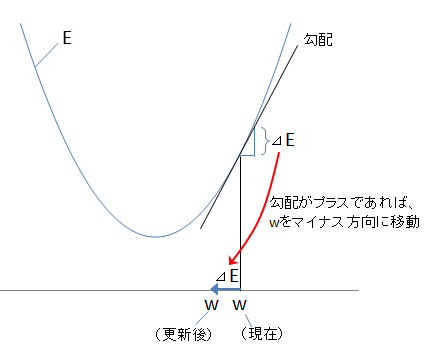
これを式で表すと、次のようになります。
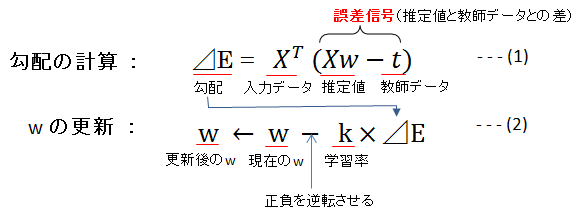
この式(1)と式(2)を繰り返し計算することにより、最も小さい \(E\) に対応する \(w\) の位置(値)を求めることができます。学習率は0.1や0.01などの固定値で、\(\Delta E\) をどの程度 \(w\) に反映させるかのパラメータです。
このように計算し、「問題2」を解くと、
\[
\begin{eqnarray}
a &=& 1.05 \\
b &=& 0.05
\end{eqnarray}
\]
となり、グラフに表すと、次のようになります。
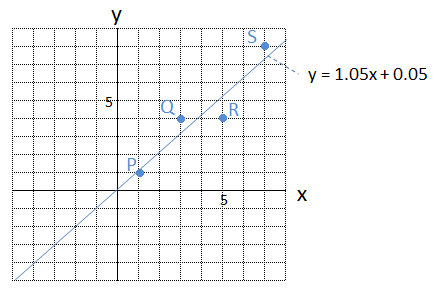
勾配降下法では、式(2)より、勾配 \(\Delta E\) さえわかれば \(w\) を更新し、正しい \(w\) を探しだすことができます。
そしてそのカギとなる勾配は、式(1)のように、誤差信号と入力データがわかれば計算できるというものです。
すなわち、推定した結果と真の値 \(y\) との「誤差」と、「入力データx」 がわかれば、パラメータ \(w\) を計算できることになります。
さて、今回は1次関数を用いて簡単なニューラルネットワークを考えましたが、この延長として、まったく同じような考え方で、次のような複数のユニットを持つニューラルネットワークを作成することもできます。
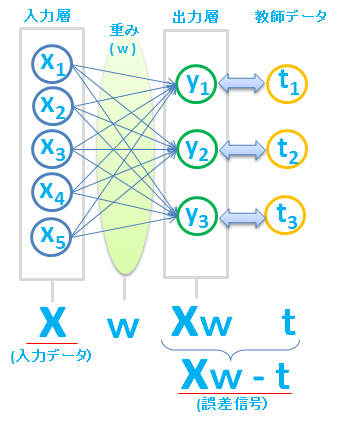
ここでは、推定した結果 \(Xw\) と真の値 \(t\) との「誤差」を、誤差信号とよんでいます。
誤差信号( \(Xw\ -\ t\) )と入力データ \(X\) から \(w\) を更新します。
更新された \(w\) を用いて、再び誤差信号を計算し、その誤差信号と入力データ \(x\) から、また \(w\) を更新する、ということを、何回も繰り返します。
誤差逆伝播法と伝言ゲーム
さらに、入力層と出力層の間に隠れ層をいれることもできます。隠れ層を何重にもすると、ディープ(深層)なニューラルネットワークができあがりますね。
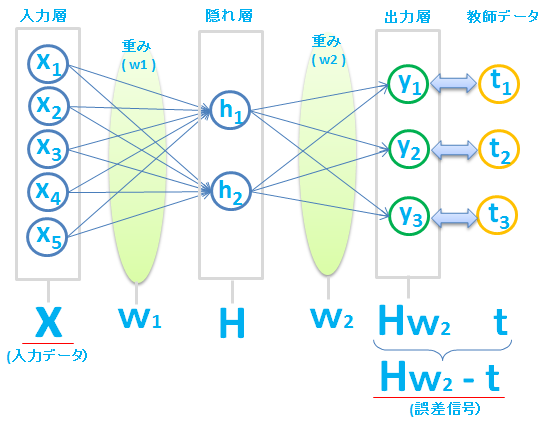
これまでと同じように、重み \(w\) を求めたいのですが、今回は \(w\) が2種類( \(w_1\)、\(w_2\) )あります。
重み \(w_1\) と \(w_2\) の両方を同時に更新する必要があります。
重み \(w_2\) は、隠れ層のデータ \(H\)(これを入力データとして考えます) と、誤差信号( \(Hw_2\ -\ t\) )から更新することができます。
ところが、重み \(w_1\) は、入力データ \(X\) はありますが、隠れ層Hの誤差信号がわからないので、このままでは重み \(w_1\) を更新することができません。
そこで、隠れ層 \(H\) の誤差信号の大きさを、なんとか求めることにしましょう。
今わかっている誤差は、出力層の誤差信号( \(Hw_2\ -\ t\) )です。
この出力層の誤差信号は、もともと隠れ層 \(H\) にあった誤差に、重みw2をかけた結果でてきた誤差とも考えられます。
このアイデアをもとに、出力層の誤差信号と \(w_2\) から逆算して、隠れ層の誤差信号を求めようというのです。
すなわち、隠れ層の誤差信号を、次のような計算で求めます。
![]()
これは、多層な場合でも、ある層の誤差信号がわかれば、(それぞれの現在の \(w\) はわかっているので)その1つ前の層の誤差信号を、次のように自動的に計算できることを表しています。
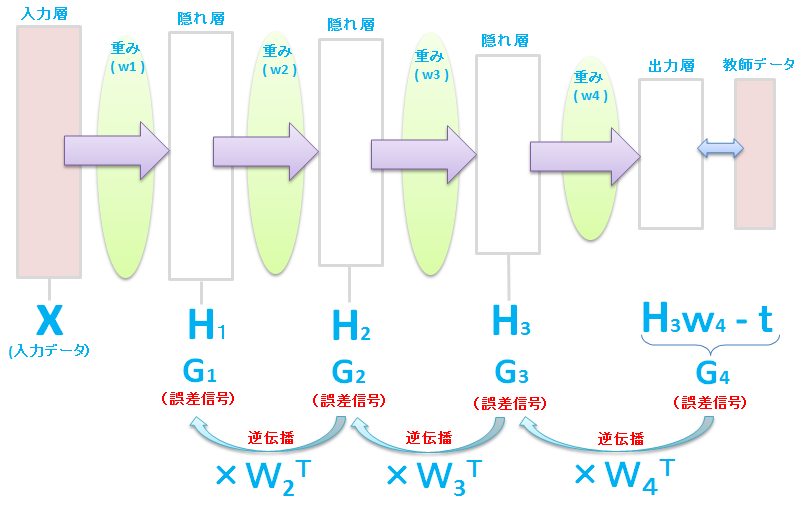
このように誤算信号は、最後の出力層側から、順次、入力層の方向に計算して求めていきます。
この方法は、誤差を逆方向に伝播させて前の層の誤差を算出することから、誤差逆伝播法(Backpropagation/backwards propagation of errors)と呼ばれています。
上記の例だと、\(H_1\) 層の誤差信号は、誤差信号 \(G_4\) にそれぞれの重み \(w\) を3回もかけて、さかのぼって計算しています。もし10層のニューラルネットワークだと、入力層の次の隠れ層の誤差信号は、計8回、重みをかけて、さかのぼって計算することになります。
誤差の逆伝播は、伝言ゲームのようなものです。もし間に8人も人が入れば、まともな話も最後はどうなるものか。。。。。
まったく当てにならないですよね。
このため、何層もあるディープなニューラルネットワークは使いものにならない、と2000年頃までは言われていました。
多層ニューラルネットワーク(ディープラーニング)への対応
そこに彗星のように現れたのがトロント大学のヒントン氏です。
ヒントン氏はGoogleにも所属しています。
ヒントン氏は、オートエンコーダやRBM(制約付きボルツマンマシン)といった仕組みを利用し、多層のニューラルネットワークでも精度を損なわない方法(事前学習方式)を提案しました。
それが現在のディープラーニングのブームにつながっています。
今では、ヒントン氏が論文をだすたびに、世界中の研究者たちがこぞってそれを読み漁るという状況です。
Googleが発表した Deep Q-Net は衝撃的でした。
Deep Q-Netは、ディープラーニングを強化学習で行なうというものです。
テレビゲームを機械に行わせ、成功、失敗を自動的にディープラーニングに強化学習させるというデモで、
はじめは失敗だらけの機会が、数時間もするとゲームの達人に近い操作が可能になるという内容でした。
~Deep Q-Netに関連するブログ~
「強化学習で〇×ゲームに強いコンピュータを育てる(深層学習 Deep Learning)」
「ネズミを追いかける振り子と機械の自動操作(深層強化学習 Deep Reinforcement Learning)」
「強化学習でボールを自由に動かす ~ネズミを追いかけるボール Part 1~ (深層学習 Deep Reinforcement Learning )」
もし、強化学習で車の運転を機械に覚えさせることができれば、将来、車の自動運転も可能になるかもしれません。自動運転機能付の車は、安全性が高いので保険料も安くなるかもしれません。
ディープラーニングは、世の中を変える1つになりそうです。今後がとても楽しみですね。
